Table of Contents
Fatigue performance description
Fatigue is a complex material phenomenon, highly nonlinear and stochastic. For mechanical design purposes, the fatigue performance of a material is described by:
- the fatigue life (denoted by N), which is the number of cycles with given stress amplitude that the part may sustain before failure, and
- the fatigue strength S, which is the highest stress that a material can withstand for a given number of cycles without breaking.
There is an established opinion that some metals, and in particular, steel and titanium, may sustain infinite number of fatigue cycles of stresses if their amplitude is below the limiting value that is called fatigue limit (denoted by FL). While there are research that suggest that fatigue limits do not exist, the fatigue strength of such materials is, for mechanical design purposes, usually described in terms of fatigue life in finite life domain (for stresses higher than the fatigue limit, S>FL) and fatigue life in infinite life domain (for stresses lower than the fatigue limit, S<FL).
The fatigue strength of a material in the finite life domain is usually described by its Wöhler (or S-N) curve, which represents dependence of the fatigue life on the amplitude of the variable stress in finite life domain. The Wöhler curve is determined by fitting the experimental data to the theoretical expressions. Both the experimental procedure and the fitting procedure are defined by standards.
Experimental tests according to ISO 1143 standard
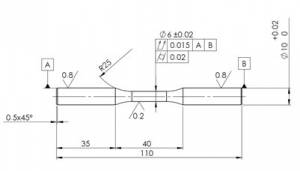
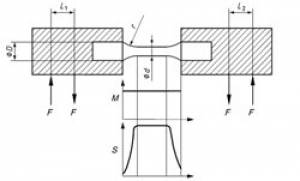
The fatigue tests in the A_MADAM project were performed according to the ISO 1143 standard, which specifies the experimental method for fatigue testing of metallic materials using bending of rotating bars. The specifications describe the accuracy of the testing apparatus, the testing procedure and presentation of the fatigue testing results. The standard defines also in details the shape (shown in figure left below), dimensions and preparation of the samples, which consist of two mounting heads and a gage between them. During a test, a sample rotates under a constant bending moment (shown in figure right below) over the gage. As a consequence, the sample undergoes cyclic symmetric loading with frequency equal to the rotation speed, and the loading conditions generate fatigue load at the sample gage. Test is carried out until the sample breaks (“failure”) or until a pre-determined number of loading cycles is achieved without failure of the sample (“run-out”). The run-out criterion in A_MADAM project was set to be 107 cycles without failure, which is usual for fatigue testing of steels. The experimental data gathered through the test are the fatigue stress to which a sample was exposed (denoted as S) and the corresponding number of the stress cycles to the failure (denoted as N), which are presented in the form of the standard Wöhler’s (or S-N) curve.
Wohler curve and fatigue limit according to ISO-12107 standard
It is well known that the results of fatigues tests performed according to the ISO-1143 display significant variations even when the test is controlled very accurately, and the main reason is difference between the test samples. The fatigue is a complex phenomenon, and even small random variations of chemical composition and microstructure profoundly affect fatigue resistance of a sample. It is for those reasons that statistical methodology had to be developed not only for analyses of the experimental data, but also for planning of the fatigue testing campaigns. The ISO-12107 standard presents methods for the experimental planning of fatigue testing and the statistical analysis of the resulting data. Its declared purpose is to determine the fatigue properties of metallic materials with high degree of confidence using a reasonably small number of specimens. The fatigue properties analysed by the methodology presented in the ISO-12107 standard are the fatigue life for a given stress level and the fatigue strength for a given fatigue life.
According to 12107, the fatigue resistance of a material in the finite life domain may be represented by the Wöhler (or S-N ) curve, which uses a linear mathematical model of the form
x = b - a·y
where x = log(N) and y = S or y = log(S), whichever gives better plot linearity, and a and b are constants obtained by fitting of the experimental results; in the previous equation, “log” represents logarithm for base ten. The previous equation is frequently written in the form
S·Nn = A
where n = 1 / a and A = b / a.
From the previous expressions, the Wöhler curve in D4AM Wiki is expressed by
Dependency of stress amplitude S on number of cycles to failure N
(so called Basquin equation)
S = A·N-n
and
Dependency of number of cycles to failure N on stress amplitude S
N = N0·S-1/n
The fatigue testing in the project A_MADAM was aimed at the determination of both the S-N curve in the finite life domain and the fatigue limits (FL). A staircase method was applied to determine the FL: for this purpose, the series of failure and not-failure events was processed by the Dixon method. A life duration of 107 cycles was set as run-out, based on previous data in the literature and on the preliminary experience of the research group with regard to fatigue testing. The Dixon method is an abbreviated staircase method that makes it possible to estimate the fatigue limit, as a result of the processing of a shorter failure-not failure sequence with respect to requirements of the international standard.