Table of Contents
Fracture resistance description
The key task of the fracture mechanics is to distinguish between the material flaws that do not grow (hence, those who are safe from the point of view of exploitation) from the material flaws that further propagate as a crack (hence those will lead to failure of the flawed structure). To that purpose, fracture mechanics defines parameters that describe both the material and the loading state of the structure, and establishes the criteria for prediction of the outcomes of loading of flawed structures.
Linear elastic fracture mechanics
In the cases when the plastic deformation zone around crack tip is much smaller than crack length, the crack propagation may be studied within the limits of elasticity (linear elastic fracture mechanics). In that case the stress fields in the structure may be expressed using a scaling factor that is called stress intensity factor (abbreviates also as SIF) K, which depends on the loading state. If the polar coordinate system is established with origin at crack tip, with polar axis x in the direction of the crack (y-axis normal to the plane of crack, and z-axis in the plane of the crack), then the linear elastic theory predicts spatial distribution of stress in the form:
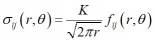 It has been shown that the SFI for any loading state may be represented by combination of stress intensity factors of three loading states, shown in the following figure:
It has been shown that the SFI for any loading state may be represented by combination of stress intensity factors of three loading states, shown in the following figure:
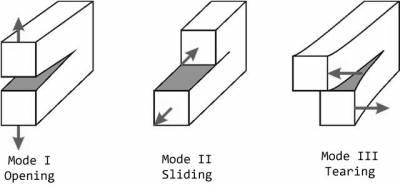 The corresponding SIF are denoted as KI, KII and KIII, and they are defined as:
The corresponding SIF are denoted as KI, KII and KIII, and they are defined as:
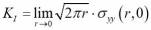
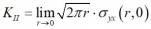
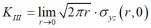 Different theoretical methods (G-criterion, Local stress criterion, Maximal tensile stress criterion, Generalized tensile stress criterion) combine the three SIFs to calculate the corresponding SFI, which is the compared to its critical value, fracture toughness Kc, where K>Kc predicts rapid and unlimited propagation of the crack and failure of the structure. Fracture toughness is expressed in terms of the critical value of stress intensity factor in mode I loading, measured under plane strain conditions, KIc, which is also known as the plane strain fracture toughness.
Different theoretical methods (G-criterion, Local stress criterion, Maximal tensile stress criterion, Generalized tensile stress criterion) combine the three SIFs to calculate the corresponding SFI, which is the compared to its critical value, fracture toughness Kc, where K>Kc predicts rapid and unlimited propagation of the crack and failure of the structure. Fracture toughness is expressed in terms of the critical value of stress intensity factor in mode I loading, measured under plane strain conditions, KIc, which is also known as the plane strain fracture toughness.
Plastic elastic fracture mechanics
In the cases when the plastic deformation zone around crack tip is of the order of the crack length, the crack propagation may not be studied within the limits of elasticity, and the loading state is described using the methods of plastic elastic fracture mechanics. The measure of the stress state and the criterion for failure of the structure is described in the terms of J-integral, which is the integral over path Γ defined as:
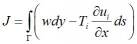 with w being strain energy density given as
with w being strain energy density given as 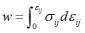 , Ti the components of surface traction vector, ui are the components of the displacement vectors, ds is an infinitesimal displacement along the path Γ, σij and εij are the stress and strain tensors.
, Ti the components of surface traction vector, ui are the components of the displacement vectors, ds is an infinitesimal displacement along the path Γ, σij and εij are the stress and strain tensors.
J-integral is calculated over a path Γ that circumvents the crack, and its value is, within the frameworks of monotonic plastic deformation theory, independent on the path. The criterion for the failure of the structure is J>Jc, where the critical value of the J-integral Jc may be calculated as
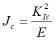 for plane stress and
for plane stress and 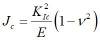 for plain strain.
for plain strain.
