Table of Contents
DMLS/SLM: Fracture resistance
This page is the entry point of the future section dedicated to description of fatigue resistance of DMLS/SLM materials. In the initial version, it contains the results of studies of fracture resistance of MS1 steel in the A_MADAM project.
Fracture resistance of MS1 steel
Fracture resistance of MS1 steel is determined experimentally, using the Inclined Edge Cracked Semi-Circular Bend (IACSB) specimen subjected to three-point bend loading.
In order to obtain the various combinations of modes, only the parameters S2/R and α were varied in the testing campaign of A_MADAM project, while S2 was kept fixed at 42 mm, and the values of t, R and a were the same for all the specimens (t=6mm, R=60 mm, a=24 mm). The various combinations of S2/R and α were used to achieve the fracture modes Mode I, Mode II and mixed modes I-II. When the bottom supports are located symmetrically to the crack line (i.e., when S1 = S2) and the crack line is in the same direction as the load (i.e., when α = 0°), the specimen is subjected to Mode I (opening mode). To obtain mixed mode I-II or Mode II (sliding mode), an appropriate combination of S1/R and α should be chosen.
Stress intensity factor (SFI) values were determined using two methods:
- Critical Fracture Load (PCR) Method
- Fitting of the displacement field measured by digital image correlation (DIC) method to Williams theoretical model
The following table presents the obtained results for KI and KII. For explanation of the variables please see the explanation of the experimental method,
| Configuration | PCR | DIC | ||||
|---|---|---|---|---|---|---|
| α (deg) | S1 (mm) | S2 (mm) | KI (MPa·m-1/2) | KII (MPa·m-1/2) | KI (MPa·m-1/2) | KII (MPa·m-1/2) |
| 0 | 42 | 42 | 44.7 | 0.0 | 75.0 | 0.2 |
| 10 | 42 | 44.7 | 16.6 | 69,0 | 19.0 | |
| 18 | 34.8 | 37.3 | 42,4 | 43.8 | ||
| 10.2 | 14.4 | 79.0 | 14.7 | 77.8 | ||
Fracture criterium
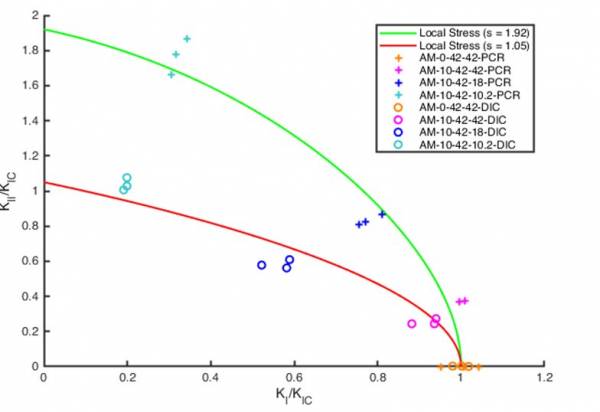
The obtained results may be explained by the multiaxial fracture model that introduces local stress (LS) criterium. Classical criteria, based on maximum tangential stress, such as the generalized maximum tangential stress (GMTS), can only predict fracture toughness of brittle materials. On the other hand, a major advantage of the LS criterium is that it can be applied to different materials (brittle and ductile), which experience either shear or tensile dominated crack propagation. Therefore, this model can be suitable for the strong, but at the same time ductile, maraging steel MS1. The LS mixed mode criterium is described by the following equation
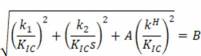 with s = KIIC/KIC, then
with s = KIIC/KIC, then
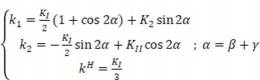
The material parameter s is related to the material ductility and affects the critical plane orientation. If the parameter s is higher than 1, as in this case, then A = 9(s2−1), B = s and γ = 0. The previous equation represents the implicit curve of the LS criterium, and the coefficient s can be determined numerically by fitting the experimental SIFs normalized to the KIC=44.7MPa·m-1/2.
The following figure illustrates the applicability of the criterion, with the red line (s=1.05, KIIC=46.9MPa·m-1/2) being fit to data obtained the Critical Fracture Load (PCR) method (empty circles), and green line (s=1.95, KIIC=87.2MPa·m−1/2) fit to data obtained by Fitting of the displacement field obtained by DIC (full circles).